Configuración Electrónica de los Elementos
La definición de configuración electrónica se entiende como la distribución de electrones en los niveles de energía y subniveles de un átomo. Esta distribución electrónica es como una huella digital que distingue un elemento de otro.
¿Qué es la configuración electrónica?
Para comprenderla plenamente, debemos analizar la estructura básica de un átomo.
Estructura del Átomo
Un átomo está compuesto por un núcleo central, que contiene protones y neutrones, rodeado por electrones en órbita. Los electrones se organizan en diferentes niveles de energía, conocidos como capas o niveles.
Niveles de Energía
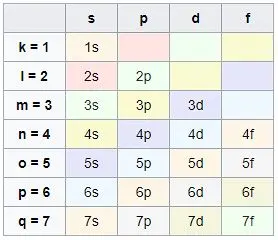
En el ámbito de la química, los electrones se distribuyen en niveles de energía, que se representan con números enteros (1, 2, 3, etc.). Cuanto más cerca esté el nivel de energía del núcleo, mayor será su energía y capacidad para retener electrones.
Subniveles
Cada nivel de energía se divide en subniveles, que se designan con letras (s, p, d, f). Dentro de estos subniveles, se encuentra el poco conocido pero teóricamente posible subnivel g, que tendría una mayor capacidad de electrones que los subniveles anteriores. Estos subniveles tienen una capacidad máxima de electrones, y la distribución en ellos sigue reglas específicas.
Reglas para la Distribución Electrónica
Ahora que tenemos una idea de qué es configuración electrónica, es importante conocer las reglas que rigen la distribución de electrones en los subniveles de energía.
Regla de Aufbau
La regla de Aufbau establece que los electrones llenan primero los subniveles de menor energía antes de pasar a los de mayor energía. Esto implica que el subnivel s se llena antes que el p, el p antes que el d y el d antes que el f.
Principio de Exclusión de Pauli
El principio de exclusión de Pauli establece que no puede haber dos electrones en el mismo átomo con los mismos cuatro números cuánticos idénticos. Esto significa que los electrones en un subnivel deben tener espines opuestos.
Regla de Hund
La regla de Hund establece que los electrones llenan todos los orbitales de un subnivel antes de emparejarse en el mismo orbital. Esto minimiza la repulsión electrónica y, por lo tanto, la energía del átomo.
Regla de Moller
Para realizar la configuración electrónica de un elemento, primero se deben ordenar los niveles de energía, definir los subniveles y luego repartir los electrones. Sugiere seguir un diagrama que compartimos más adelante.
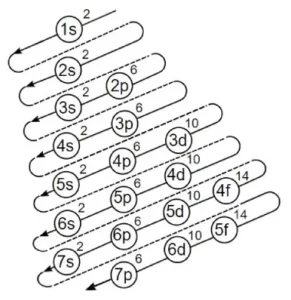
Al hablar de la distribución electrónica, es fundamental entender qué es el diagrama de Linus Pauling, una herramienta visual que ayuda a determinar el orden de llenado de los orbitales atómicos.
En cuanto a las 4 reglas básicas, tenemos las siguientes:
- El valor de los electrones es igual al número atómico del elemento. Dicho valor es el primero que debes conocer para realizar la distribución.
- Para representar la configuración electrónica se consideran los niveles de energía (1, 2, 3…) y los subniveles (s,p,d,f).
- Se distribuyen los electrones en cada subnivel.
- Se debe respetar la cantidad máxima que pueden soportar según las teorías y el diagrama de Linus Pauling, también conocida como la regla de las diagonales.
Tabla de configuración electrónica
Aquí tienes la lista completa de la configuración electrónica de todos los elementos de la tabla periódica para que puedas descargarla en .pdf e imprimirla.
¿Para qué sirve?
El uso de la configuración electrónica de un elemento químico puede variar, sin embargo, la más importante es que permite conocer la reactividad que tiene cada elemento. En otras palabras, la configuración electrónica nos ayuda a saber cuál es la capacidad que tiene un elemento químico para combinarse con otro elemento.
Es así cómo se logra crear una gran cantidad de compuestos, ya que podemos conocer la cantidad de electrones que puede ceder un elemento químico para volverse uno con un segundo elemento.
Teóricamente, esta configuración nos permite determinar la posición que ocupa cada elemento dentro de la tabla periódica. Es una forma de conocer más acerca de las características de cada elemento y sus propiedades, que en términos generales nos ayuda a conocer más acerca de los fenómenos físicos, químicos y naturales de la vida.
Si consideras estos pasos, podrás verificar que el resultado de tu distribución electrónica será idéntica a la sugerida oficialmente para cada elemento químico de la tabla periódica.
Ejemplo de Configuración Electrónica
Tomemos el ejemplo del carbono (C). Tiene 6 electrones y su configuración electrónica es 1s² 2s² 2p². Esto significa que hay 2 electrones en el nivel 1 (1s²) y 4 en el nivel 2 (2s² 2p²). Esta configuración es crucial para comprender cómo el carbono forma enlaces y participa en reacciones químicas.
Aquí tienes la lista completa de la configuración electrónica de todos los elementos de la tabla periódica para que puedas descargarla en .pdf e imprimirla.
Punto de ebullición de un elemento
Masa atómica de un elemento
Estados de agregación de la materia en la tabla periódicaEsperamos que te haya gustado este artículo sobre Configuración Electrónica de los Elementos.
